• [前のページ]
• [目次]
• [1]
• [2]
• [3]
• [4]
• [5]
• [6]
• [7]
• [8]
• [9]
• [次のページ]

ケルンのフランコ著『計量音楽論』第五章、第六章

●第五章

Capitulum 5: De ordinatione figurarum adinvicem.

第五章：フィグラの相互の並び方について

Simplicium autem valoris cognitio ex ordinatione quam habent adinvicem declaratur. Ordinatio vero earum sic accipitur: aut enim longam sequitur longa, aut brevis; et nota hoc idem esse iudicium de brevibus et semibrevibus. Si autem longam longa sequatur, tunc prima longa sub uno accentu tribus temporibus mensuratur et perfecta longa nuncupatur, sive sit figura vel pausa, ut hic:

単独のフィグラ(音符)の音価は相互の並び方によって明示される。実に、それらの並び方は、以下のように把握される：ロンガに、ロンガが続くかブレヴィスが続くかというふうに。また、同様にこれはブレヴィスとセミブレヴィスについての判定法でもあることに注意せよ。もし、ロンガの後にロンガが続いたら、第一のロンガは三つのテンプスで一つの音調として計量され、完全ロンガと呼ばれる。それはフィグラ(音符)であっても休止(休符)であってもよい。このように：

Si vero longam sequatur brevis, hoc est multipliciter, quoniam sola vel plures. Si sola, tunc longa est duorum temporum et dicitur imperfecta, ut hic:
.
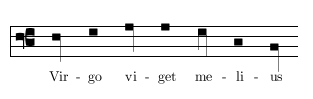Nisi inter illas duas, scilicet longam et brevem, ponatur quidam tractulus qui signum perfectionis dicitur, qui etiam alio nomine divisio modi appellatur; et tunc longa prima perfecta est, et brevis imperficit sequentem longam, ut hic:
.

もしロンガの後にブレヴィスが続くなら、それが一つか複数かによって、様々である。 もし一つなら、ロンガはテンプス二つ分であり、不完全と呼ばれる。このように：

.
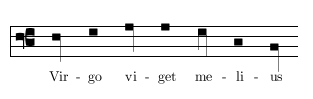
もしこれら二つ、すなわちロンガとブレヴィス、の間に、完全化記号 signum perfectionis と呼ばれる、あるいはディヴィジオ・モディ divisio modi という別の名前でも呼ばれる、小さな垂線が置かれていないかぎりにおいて。そして、このとき(完全化記号が置かれているとき)は、第一のロンガは完全であり、ブレヴィスは後続するロンガを不完全化する。このように：

.

Si autem plures, hoc est multipliciter: aut duae, aut tres, aut quatuor, aut quinque, aut plures quam quinque. Si duae tantum, ut hic:
,
tunc longa est perfecta, nisi eam sola brevis praecedat, ut hic:
.

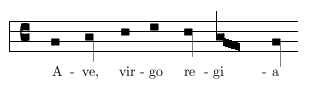一方、もし(ブレヴィスが)複数あったら、これは様々である： 二つ、あるいは三つ、あるいは四つ、あるいは五つ以上かによって。もし、ちょうど二つだったなら、このように：

,
このときロンガは完全である、一つのブレヴィスがそれに先行しないかぎり、このように：
.

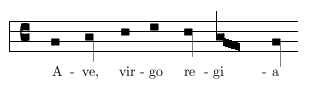
Duarum autem brevium prima recta, secunda vero altera brevis appellatur. Recta brevis est quae unum solum tempus continet; altera autem brevis similis est longae imperfectae in valore, differens tamen in figuratione. Nam utraque sub diversa figuratione duobus temporibus mensuratur. Unum tempus appellatur illud quod est minimum in plenitudine vocis.

一方、二つのブレヴィスの第一のものはレクタ・ブレヴィス、二番目はアルテラ・ブレヴィスと呼ばれる。レクタ・ブレヴィスはただ一つのテンプスしか含まないものである。一方、アルテラ・ブレヴィスは音価において不完全ロンガと同じで、にもかかわらず形態において異なる。というのは、異なる形態のもとで、どちらもテンプス二つ分と計量されるからである。テンプス一つ分は、音 vox の十全性における最小であるもののことを言う。

Si vero inter praedictas duas breves ille tractus qui divisio modi dicitur apponatur, ut hic:

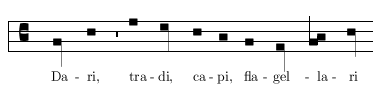
tunc longa prima est imperfecta et etiam secunda; brevium autem ipsarum quaelibet erit recta: hoc tamen rarissime invenitur.

もし、前述の二つのブレヴィスの間にディヴィジオ・モディと呼ばれる線が置かれているなら、このように：


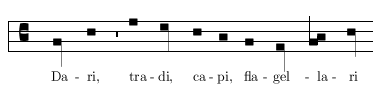
そのときは、第一のロンガは不完全であり、第二もまたそうである。一方、ブレヴィスそれ自身はどちらもレクタになるだろう。しかし、これは最も稀にしか見られない。

Si tres breves tantum inter duas longas accipiantur, ut hic:

idem quod prius habetur, nisi quod illa quae primo altera brevis dicebatur, hic in duas rectas breves separatur.

もし、二つのロンガの間に三つのブレヴィスが入れられているならば、このように：


前のことが同様にあてはまるが、最初にアルテラ・ブレヴィスと呼ばれていたものは、ここで二つのレクタ・ブレヴィスに分けられる。

Sed si inter primam brevem et duas sequentes divisio modi apponatur, ut hic:

tunc prima longa a prima brevi imperficitur; secundarum brevium sequentium prima fit recta, ultima vero alteratur. Et nota quod tria tempora, tam uno accentu quam diversis prolata, unam perfectionem constituunt.

しかし、もし最初のブレヴィスとそれに続く二つの(ブレヴィス)の間にディヴィジオ・モディが置かれているなら、このように：


最初のロンガは最初のブレヴィスによって不完全化される。その次に続くブレヴィスたちのうち最初のものはレクタになり、最後のものはアルテラ化される。

Si plures quam tres, ut hic:
,
tunc prima semper est imperfecta, nisi ei signum perfectionis addatur, ut hic:
.^*1

もし三つより多くブレヴィスがあるなら、このように：

,
そのときは、第一のロンガは常に不完全である。完全化記号が付け加えられない限り、このように：
^*1
.

註：

*1 Gratissimum pro reatu [nostro]

この例には、完全化記号はありますが、「二つのロンガの間に」「三つより多いブレヴィス」があるわけではないので例としては不十分だと思います。 [Back]

Sequentium autem brevium quaelibet est recta, si in computando in ternario numero, quo constituitur perfectio, inveniatur. Sed si duae tantum in fine remaneant, tunc ultima earum altera brevis dicitur, ut hic:
.
Si vero sola, erit recta, et ultimam longam imperfectam reddit, ut hic:
.

一方、(いくつも)続くブレヴィスはどれもが、もし、合計して、それによって完全が形成される、３になるならば、レクタである。しかし、もし、ちょうど二つが終わりに残ったなら、それらの最後のものはアルテラ・ブレヴィスになる。このように：

.
もし、ちょうど一つだけ残ったなら、それはレクタであろう。また、それは最後のロンガを不完全にする。このように：

.

De semibrevibus autem et brevibus idem est iudicium in regulis prius dictis. Sed nota semibrevium plures quam tres pro recta brevi non posse accipi, quarum quaelibet minor semibrevis dicitur, eo quod minima pars est ipsius rectae brevis, ut hic:

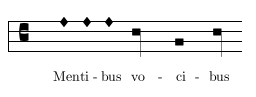
nec minus quam duas, quarum prima minor, secunda maior semibrevis appellatur. Secunda maior pro tanto dicitur, quia duas minores in se includit, ut hic:
.

しかし、レクタ・ブレヴィスに関して三つより多いセミブレヴィスは許容されえないことに注意せよ。これらのどれもが、ミノル・セミブレヴィス minor semibrevis と呼ばれる。それは、レクタ・ブレヴィス自身の最小の部分である。このように：


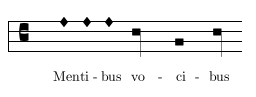
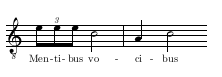
また、(レクタ・ブレヴィスに関して)二つより少ないセミブレヴィスは許容されえないことに注意せよ。これらの最初のものはミノル・セミブレヴィス、第二のものはマヨル・セミブレヴィス maior semibrevis と呼ばれる。第二のものはかくしてマヨルと言われる。なぜならば、(それは)それの内に二つのミノルを含むからである。このように：

.

Sed si immediate duae semibreves, pro recta brevi positae, tres sequuntur, vel e converso ut hic:

tunc divisio modi inter tres et duas, vel e converso, est ponenda, ut in praedicto exemplo apparet.

しかし、もし、(一つの)レクタ・ブレヴィスについて、置かれた二つのセミブレヴィスが、三つ(のセミブレヴィス)に続かれるなら、あるいはその逆なら、このように：


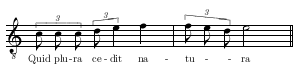
そのときは、三つと二つの間に、あるいはその逆に、デォヴィジオ・モディが置かれるべきである。前述の例において明白なように。

Pro altera autem brevi minus quam quatuor semibreves accipi non possunt, ut hic:
,
nec plures quam sex, ut hic:
^*1
eo quod altera brevis in se duas rectas includit; per quod patet quorundam mendacium, qui quandoque tres semibreves pro altera brevi ponunt, aliquando vero duas.

一方、アルテラ・ブレヴィスについて、四つよりも少ないセミブレヴィスは許容されえない。このように：

,
あるいは、六つより多くも許容されえない。このように：
^*1

というのは、アルテラ・ブレヴィスはそれの内に二つのレクタを含んでいるからである。このことから、一つのアルテラ・ブレヴィスに対して、あるときは三つのセミブレヴィスを置き、またあるときには二つを置く、という人々の誤りは明白である。

註：

*1 Ave, Maria gratia ple[n]a

この譜例の、最後から二番目のセミブレヴィスの二音のリガトゥラは、別の校訂版ではシネ・プロプリエタテ - インペルフェクツィオの二音のリガトゥラ(ロンガ - ブレヴィスのリガトゥラ)になっています。一応ここではこの譜例にもとづいて現代譜を作りました。 [Back]

●第六章

Capitulum 6: De plicis in figuris simplicibus.

第六章：単独のフィグラのなかのプリカについて

Praeterea sunt aliae quaedam figurae simplices, illud idem quod praedictae significantes, eisdem etiam nominibus cum additione huius quod est plica, nominatae.

さらに、プリカと名付けられた付加物とともに、同じ名前で、前述の単独音符たちと同じものを示す、別の単独のフィグラ(音符)たちがある。

Idcirco videndum est quid sit plica. Plica est nota divisionis eiusdem soni in grave et acutum. Plicarum alia longa, alia brevis, alia semibrevis. Sed de semibrevi ad praesens nihil intendimus, cum non in simplicibus figuris possit plica semibrevis inveniri. In ligaturis tamen et ordinationibus semibrevium plica possibilis est accipi, ut postea apparebit.

それゆえ、プリカとは何であるかを見なければならない。プリカとは、同じ音の高い方と低い方への分離の記号である。プリカの伴う音符はあるものはロンガ、あるものはブレヴィス、あるものはセミブレヴィスである。しかし、単独のフィグラのなかにセミブレヴィスのプリカは見出しえないので、セミブレヴィスについては、現時点ではなにも言わない。しかし、リガトゥラとセミブレヴィスの秩序においては、後で現れるだろうように、プリカは受け入れられることが可能である。

Item plicarum alia ascendens, alia descendens. Plica longa ascendens est quaedam quadrangularis figura, solum tractum gerens a parte dextra ascendentem, ut hic: 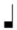, vel magis proprie duos, quorum dexter longior est sinistro, ut hic: 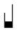. Magis proprie dico, quia per illos duos tractulos nomen plicae habere meretur.

また、プリカのあるものは上行するものであり、あるものは下行するものである。 上行するロンガ・プリカは、ある四角形のフィグラであり、右側の部分から上を向いた一つの線が出ている。このように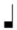： , またはより適切には、二本出ていて、その右の方が左よりも長い。このように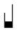：. より適切にと私は言った。なぜなら、これら二本の線のために、プリカ(折り目、襞)の名前を持つことが正当化されるのだから。

Longa vero descendens similiter duos habet tractus, sed descendentes, dextrum ut prius longiorem sinistro, ut hic: 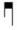. Plica brevis ascendens est quae habet duos tractus ascendentes, sinistrum tamen longiorem dextro, ut hic: 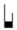. Descendens vero brevis duos tractus habet descendentes, sinistrum longiorem, ut hic: .

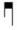下行するロンガ・プリカは、同様に二つの線を持つが、下を向いていて、前と同じように、右の方が左より長い。このように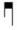：. 上行するブレヴィス・プリカは、二つの上向きの線を持ち、左が右よりも長い。このように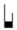：. 下降するブレヴィス・プリカは二つの下向きの線を持ち、左の方が長い。このように：.

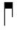Et nota istas plicas similem habere potestatem et similiter in valore regulari quemadmodum simplices supradictae.

また、これらのプリカは前に述べた単独音符と同様の力を持ち、また音価に関する規則においても同様であることに注意せよ。

→ 次のページ

• [前のページ]
• [目次]
• [1]
• [2]
• [3]
• [4]
• [5]
• [6]
• [7]
• [8]
• [9]
• [次のページ]

Last modified: 2006/9/2

• [Home]>
• [雑文のページ]